The steady flow equations can be derived from the continuity and momentum equations:
continuity:
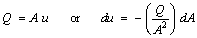
momentum:
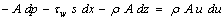
equation of state (surface tension):
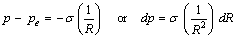
Combining and reducing:
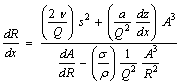
The governing steady flow equation has some interesting features.
|
|
First, the radius of curvature along the length of the flow path is easily solved by simple integration.
Second, the denominator can go to zero indicating a choking phenomenon. This is similar to choking in supersonic flow except that the limiting velocity is not the density wave propagation speed but instead the area wave propagation speed.
The force balance equation and the steady flow equation found on this page do not fully characterize vane flow. The flow transients are critical to ensuring proper vane performance. The unsteady flow equations also can be derived from the continuity and momentum equations but the solution is not as straightforward. More details about unsteady flow can be found in the reference below.
For more information on the design, use, and physics of vane flow please see
AIAA 91-2172 Propellant Management Device Conceptual Design and Analysis: Vanes
|
